Aula 4/11 | professor Manoel Cruz
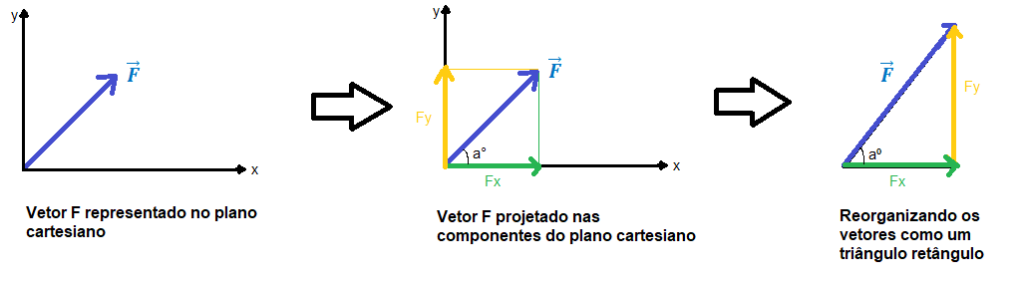
Vetor
Não é um número, indica uma força através de um elemento gráfico que possui: módulo, sentido e direção.
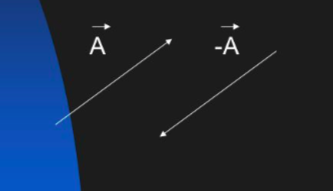
Se você conhece o vetor F e a lhe é pedido o vetor oposto, precisa trocar o sentido do vetor, mas mantém a mesma direção e o mesmo módulo.
Sistema de forças
Fr = m.a
Fr = F1 + F2 + …. + FN
Caso 1: em modo acelerado
a ≠ 0, logo Fr = m.a
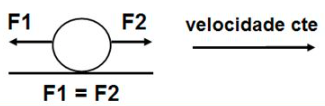
Caso 2: velocidade constante (equilíbrio dinâmico)
a = 0; v ≠ 0 constante
logo Fr = m.0, ∴ Fr = 0
Caso 3: repouso (equilíbrio estático)
a = 0; v = 0 constante
∴ Fr = 0
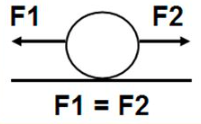
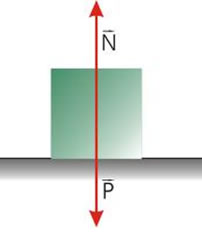
Exemplo do equilíbrio quando tem a carga força P (peso), tem um módulo no sentido oposto de força de R (reação) ou N (normal), sendo… R – P = 0 ou N – P = 0
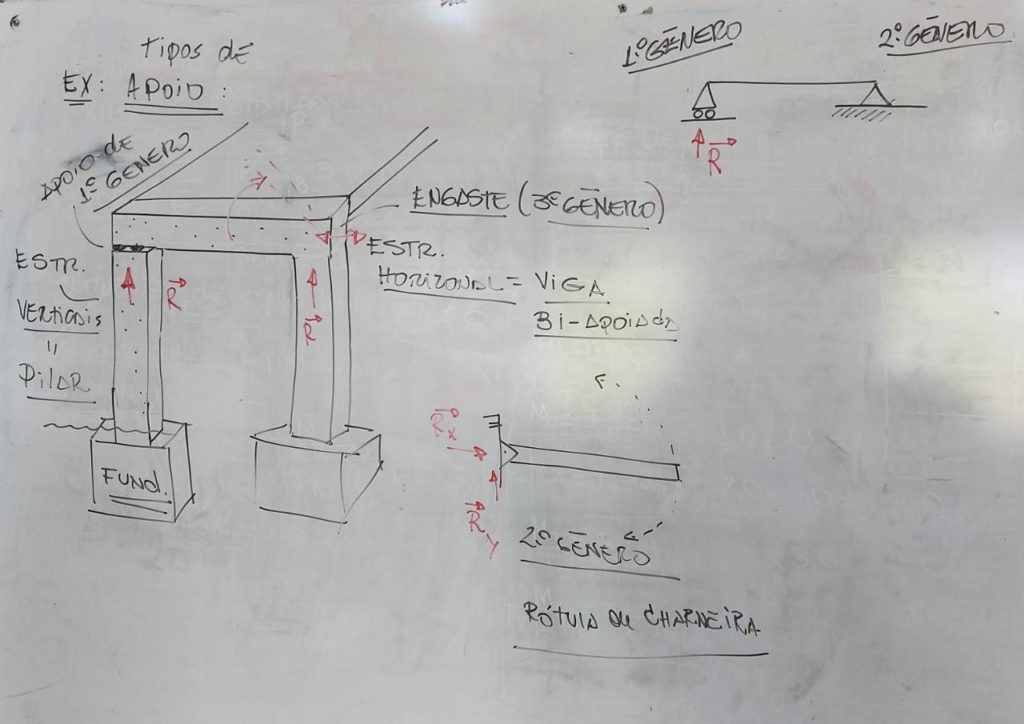
Caso 4: momento fletor (Nxm) – sistema de engaste
quando você distancia do apoio, a força é maior
quando você amplia a carga, a força é maior
o M = F . d
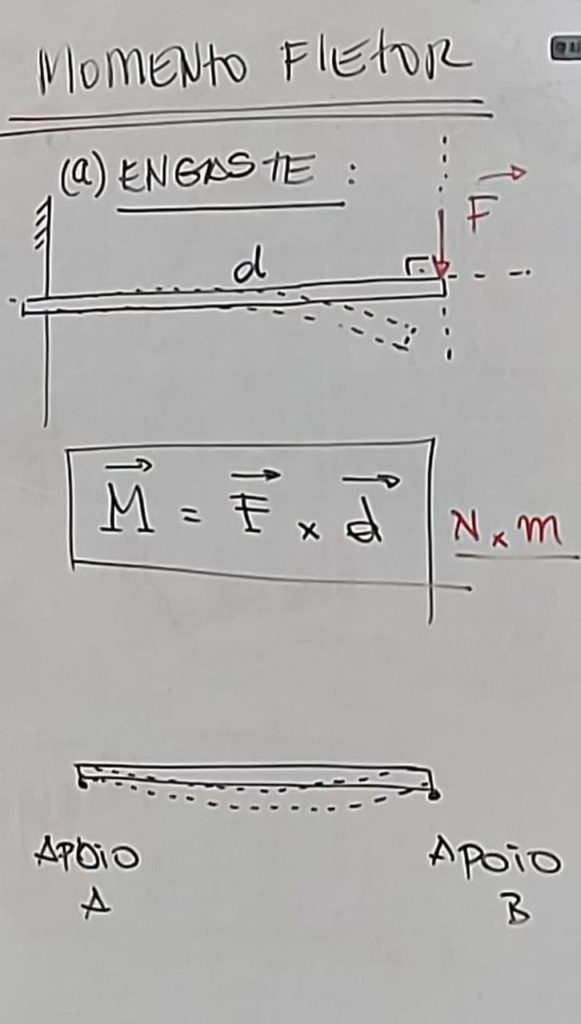
Exemplo:
Condição de equilíbrio FR = 0 , é preciso equilibrar os “momentos”
O Momento Resultante (da somatória dos momentos) precisa ser = 0
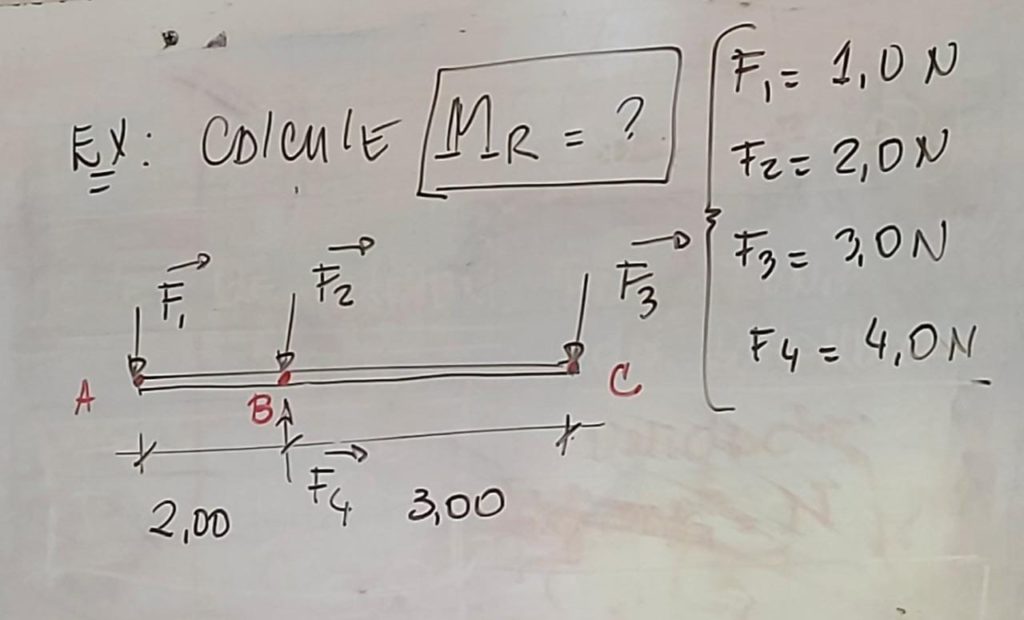
Calculando cargas pontuais ou concentradas com o apoio em ponto A
- M1 = F1 . d1 → 1 x 0 = 0 N.m
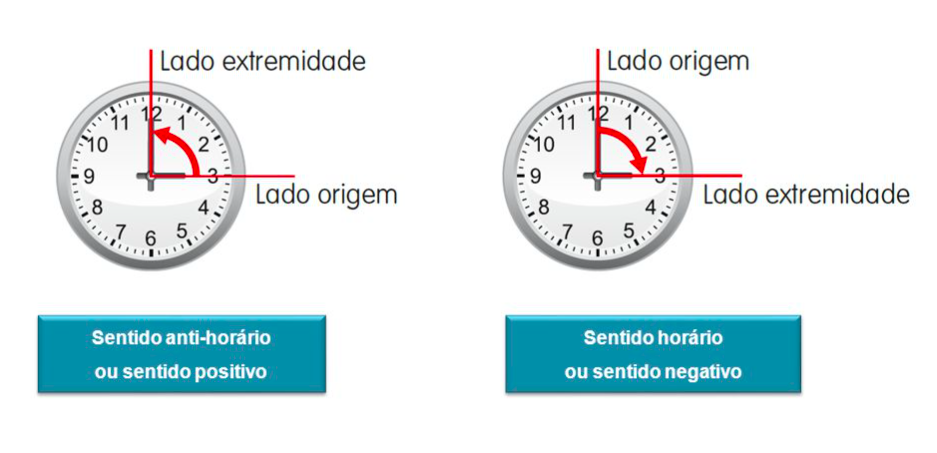
- M2 = F2. d2 → 2 x 2 = 4 N.m → (horário = negativo) → -4
- M3 = F3 . d3 → 3 x 5 = 15 N.m → (horário = negativo) → -15
- M4 = F4. d4 → 4 x 2 = 8 N.m → (antihorário = positivo) → +8
- MR = – 4 – 15 + 8 = 11 N.m (em sentido horário)
Calculando cargas pontuais ou concentradas com o apoio em ponto B
- M1 = F1 . d1 → 1 x 2 = 2 N.m → (antihorário = positivo) → +2
- M2 = F2. d2 → 2 x 0 = 0 N.m
- M3 = F3 . d3 → 3 x 3 = 9 N.m → (horário = negativo) → -9
- M4 = F4. d4 → 4 x 0 = 0 N.m
- MR = + 2 – 9 = 7 N.m (em sentido horário)
Calculando cargas pontuais ou concentradas com o apoio em ponto C
- M1 = F1 . d1 → 1 x 5 = 5 N.m → (antihorário = positivo) → + 5
- M2 = F2. d2 → 2 x 3 = 6 N.m → (antihorário = positivo) → + 6
- M3 = F3 . d3 → 3 x 0 = 0 N.m
- M4 = F4. d4 → 4 x 3 = 12 N.m → (horário = negativo) → + 12
- MR = + 5 + 6 – 12 = 1 N.m (em sentido antihorário)
Tipos de apoio:
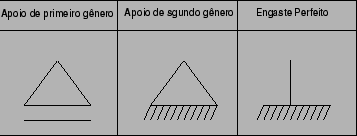
Desenho da aula:
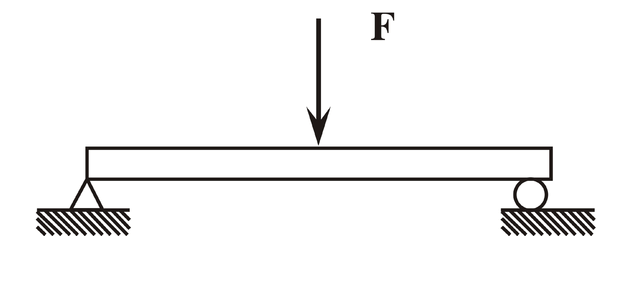
Exemplo
Viga bi-apoiada, se a carga fosse de 50 toneladas e estivesse bem no meio, 5m para um lado, 5m para o outro, cada apoio aguentaria 25 tons.
MR = 0
FR = 0
Recapitular:
1a Lei de Newton
INÉRCIA
Propriedade da matéria de resistir a qualquer variação no seu estado de movimento ou de repouso.
- Se um corpo estiver parado, permanecerá parado.
- Se um corpo estiver em movimento, permanecerá em movimento retílineo uniforme.
2a Lei de Newton
PRINCÍPIO FUNDAMENTAL DA DINÂMICA
O movimento depende de massa e aceleração.
F = m.a, no sistema internacional
- a massa é em kg
- acelaração em m/s2
- força em N (Newton)
P = m.g, sendo |g| 9,81 m/s2
3a Lei de Newton
LEI DA AÇÃO E DA REAÇÃO
Para toda força de ação que é aplicada a um corpo, surge uma força de reação em um corpo diferente. Essa força de reação tem a mesma intensidade da força de ação e atua na mesma direção, mas com sentido oposto.