Professora Lia Melo (email), aula de 16/03/2023
Termos importantes
1) Variável
Aquilo que eu vou medir, contar, mensurar
Para cada objeto de pesquisa eu tenho que escolher que variável eu vou considerar
- quantitativas: numéricas, permitindo operações matemáticas
Ex: salário, idade, peso, diâmetro, altura etc.- contínua: assume qualquer valor entre dois limites. Ex: altura, peso, volume
- discreta: só assume valores inteiros, proveniente de contagem. Ex: 1, 2, 3…
- qualitativas: não-numéricas, definem e qualificam aquele indivíduo
- nominal: os indivíduos ou elementos são classificados em categorias mutuamente exclusivas.
Ex: sexo (masculino ou feminino), cor de pele (branca, preta, amarela, parda), clima, solo, etc. - ordinal: quando os elementos são classificados em categorais que se apresentam segundo uma ordem lógica, crescente ou decrescente.
Ex: grau de instrução: sem instrução, primário incompleto, primário completo…
- nominal: os indivíduos ou elementos são classificados em categorias mutuamente exclusivas.
2) População ou Universo Estatístico
- objeto de estudo
- total dos indivíduos que se pretende fazer inferência
- o que define a população é o objetivo da pesquisa
Ex 1: determinar a produção de óleo de copaíba na região sul da Flona do Tapajós
Resp: Árvores de Copaíba no sul da Flona
Ex 2: determinar a produção (ton/ha) de soja no município de Santarém.
Resp: áreas de cultivo de soja no município de Santarém
Ex. 3: Conhecer o potencial madeireiro de uma área de 5000ha na Resex Tapajós Arapiuns
Resp: Todas as árvores com diâmetro de corte em uma área de 5000ha na Resex
Classificação das Populações
FINITAS – Existência real. Todos os componentes podem ser avaliados.
INFINITAS – Não tem existência real (teoria das probabilidades)
3) Amostra
SUBCONJUNTO FINITO – Uma amostra da população
4) Parâmetro
Valor real obtido quando toda a população é medida
5) Estimativa
Valor estimado obtido a partir da amostra
6) Medidas de Tendência Central
Medidas estatísticas que indicam o centro de um conjunto de valores
Média aritmética simples
- parâmetro – símbolo μ (Mi)
- estimativa – x
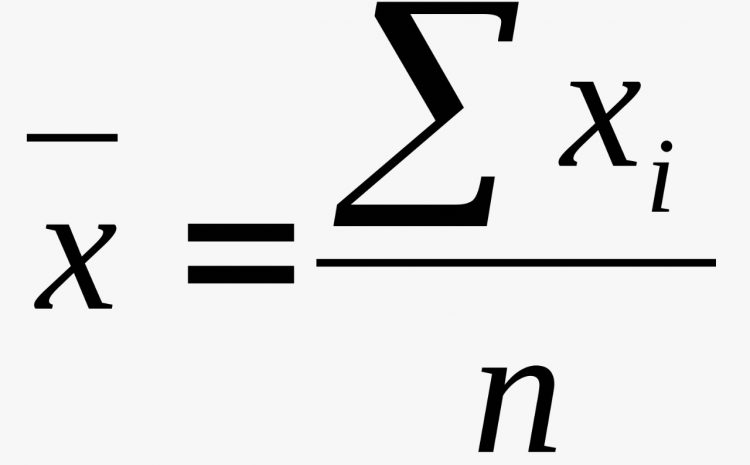
Valor que representa o conjunto de dados
- Maior utilização
- Facilidade de determinação
- Influencia por valores extremos discrepante
Exercício:
Peso em (g) de 12 ratos com 30 dias.
50, 62, 70
79, 60, 64
66, 77, 58
55, 82, 74
Somar todos os valores e dividir por 12
x = (50 + 55 + 58 + 60 + 62 + 64 + 66 + 70 + 74 + 77 + 79 + 82) / 12
x = 797 / 12
x = 66,4 g
Agora vou acrescentar mais um ratato de 250g, discrepante. Tenho que somar agora o peso dos 13 elementos e dividir por 13.
x = 797 + 250 / 13
x= 1047/13
x = 80,5g, essa média não é representativa do conjunto, porque o ratinho de 250g é discrepante dos outros e distorcendo a média.
Desvio da média
- Ver quanto cada elemento fica longe da média (numericamente).
- A soma dos desvios é sempre igual a ZERO (0)
Exercício
Número de mudas/ espécie no viveiro do IBEF
- Araracanga: 25 mudas
- Cedro: 18 mudas
- Mogno: 22 mudas
- Breu: 30 mudas
- Paricá: 15 mudas
Somar todos os valores e dividir pelos 5 tipos
x = (25 + 18 + 22 + 30 + 15) / 5
x = 22 mudas em média
| Tipo | Numero de mudas | Subtrair média | DESVIO |
|---|---|---|---|
| Araracanga | 25 | 22 | 3 |
| Cedro | 18 | 22 | -4 |
| Mogno | 22 | 22 | 0 |
| Breu | 30 | 22 | 8 |
| Parica | 15 | 22 | -7 |
| 110 | 110/5 | 0 somatória do desvio dá zero |
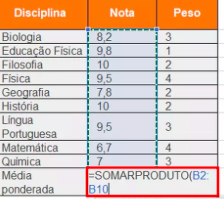
Média aritmética ponderada
Quando os valores apresentam nível de importância diferente no conjunto, com diferentes pesos.
Ex:
Moda
Valor que ocorre com maior frequência em um conjunto de daods
- usado para variáveis quantitativas discretas
- variáveis qualitativas
Ex: levantamento da presença de plantas medicinais nos quintais de uma comunidade rural
| Número de plantas medicinais | Número de quintais | QUAL A MODA |
|---|---|---|
| 0 | 5 | |
| 1 | 15 | |
| 2 | 12 | |
| 3 | 18 | a moda é ter 3 plantas por quintal, pois aconteceu em 18 quintais |
| 4 | 10 | |
| 5 | 6 |
Ex: esquisa sobre o uso do fogo para limpeza de áreas agrícolas em uma região
| Uso do fogo | Número de quintais | QUAL A MODA |
|---|---|---|
| nunca | 3 | |
| raramente | 22 | |
| às vezes | 30 | |
| com frequência | 40 | a moda é usar fogo com frequência, que aparece em 40 quintais |
| sempre | 15 | |
Mediana
Valor que ocupa a posição central em um conjunto de valores ordenados. Usada para variáveis quantitativas. Não é influenciada por valores discrepantes.
Quando n é ímpar, T = (n+1) / 2, termo de conjunto que corresponde a mediana. O valor pertence ao conjunto.
Quano n é par, T1 = n / 2 e T2 = (n+2) / 2, dois termos centrais para o cálculo da mediana, média dos dois termos. O valor não pertence ao conjunto.
Medidas de Dispersão
usadas para quantificar a variçaão de um conjunto de valores
Ex: notas de alunos
- 5 + 5 + 5 + 5 | x = 5 (não tem dispersão)
- 6 + 4 + 4 + 6 | x = 5 (dispersão pequena)
- 10 + 6 + 0 + 4 | x = 5 (dispersão intermediária)
- 0 + 0 + 10 + 10 | x = 5 (dispersão maior)
Amplitude total (AT)
AT = maior – menor valor
Exemplo: variável idade de 2 grupos de pessoas
- A = 4, 9, 11, 3 , 20, 19 — maior variação
- B = 10, 11, 3 , 11, 20, 10 — menor variação
ATA = 20 – 3 = 17 anos
ATB = 20 – 3 = 17 anos