Funções

y = f (x), sendo que x, y ∈ ℝ

Exemplo 1

f (x) = √x

Dom (f) = {x ∈ ℝ | x ≥ 0} = [0, +∞)

não existe raiz de X se X for menor que 0 → ∄ √x, se x < o

Equação que descreve o átomo de H
usa o “i” = √-1 | i² = -1
para conseguir prosseguir o raciocínio da equação

Equação de Schrödinger

Dízimas infinitas

seria 10 = 9,9999999999…?

se 10/3 = 3,3333333333…

∴ 10 = 9,9999999999…

seria 1 = 0,9999999999…?

sim, mas não é menor que 1.

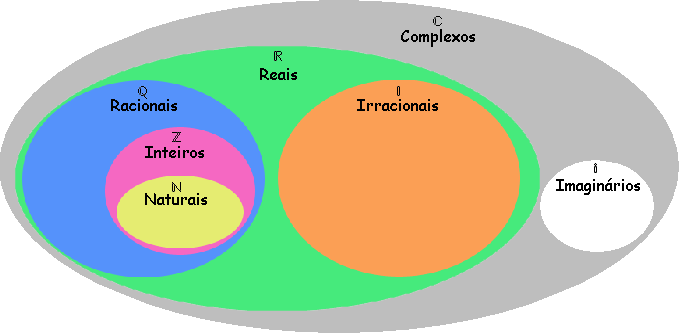
Números imaginários ou complexos

z = x + i y

• x é a parte real do número complexo z

Dom (f) = {x, y ∈ ℝ )