Função: Módulo, Simetrias

(Aula 4 – PDF de notas do professor)

• exemplos 9 e 10 no livro (páginas 16-18)

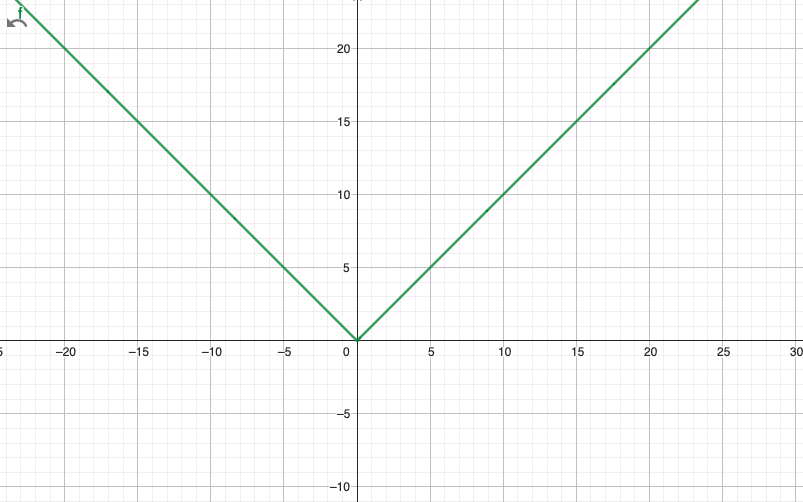
y= |x |

y = g (x) = | x |

• { x , se x ≥ 0
• { – x , se x < 0

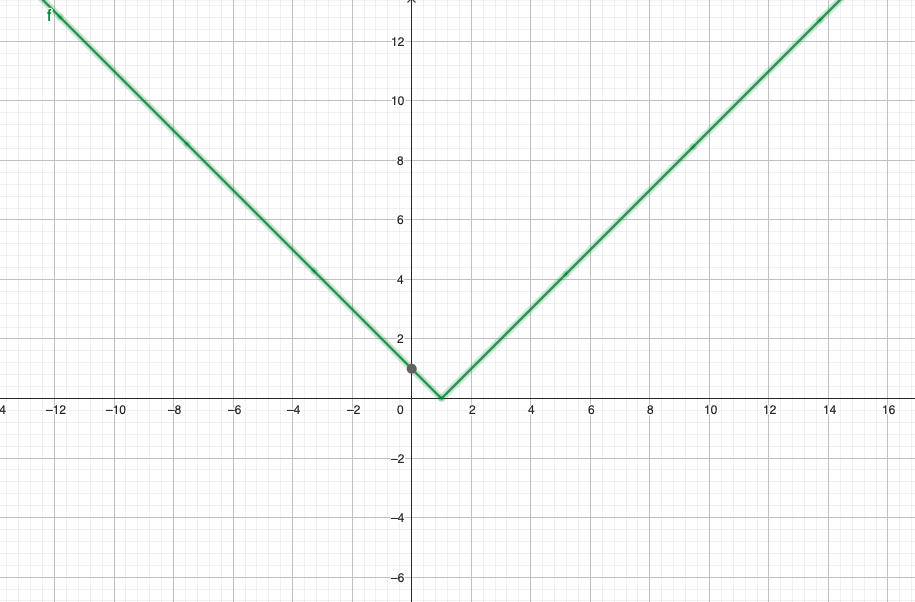
y= |x – 1|

y = g (x) = | x – 1 |

• { x – 1, se x – 1 ≥ 0
• { – ( x – 1), se x – 1 < 0

| x- 1 |

• { x – 1, se x ≥ 1
• { 1 – x, se x < 1

y = f (x) = | x |

y = g (x) = | x – 1 |

• { x – 1, se x – 1 ≥ 0
• { – ( x – 1), se x – 1 < 0

| x- 1 |

• { x – 1, se x ≥ 1
• { 1 – x, se x < 1

Simetrias

Função PAR (ex: x²)

se f (2) = 4 = f (-2)

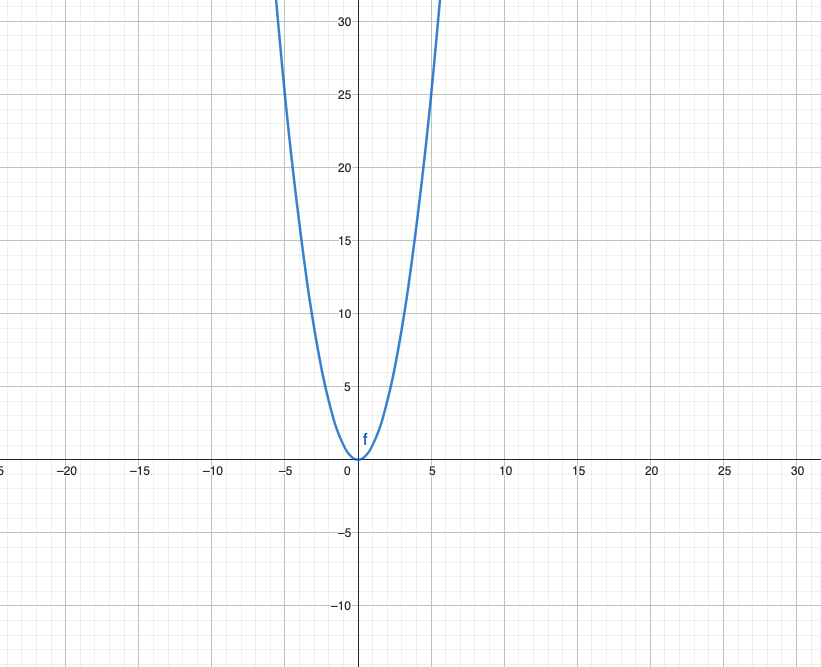
• p e p’ são equidistantes ao eixo do y
• a curva é simétrica
• o teste é ver se o f (x) = f (-x), por exemplo:
  • f (x ) = x² → 2² = 4
  • f (-x) = -x² → 2² = 4
    • os dois y (p e p’) deram 4

Função ÍMPAR (ex: x³)

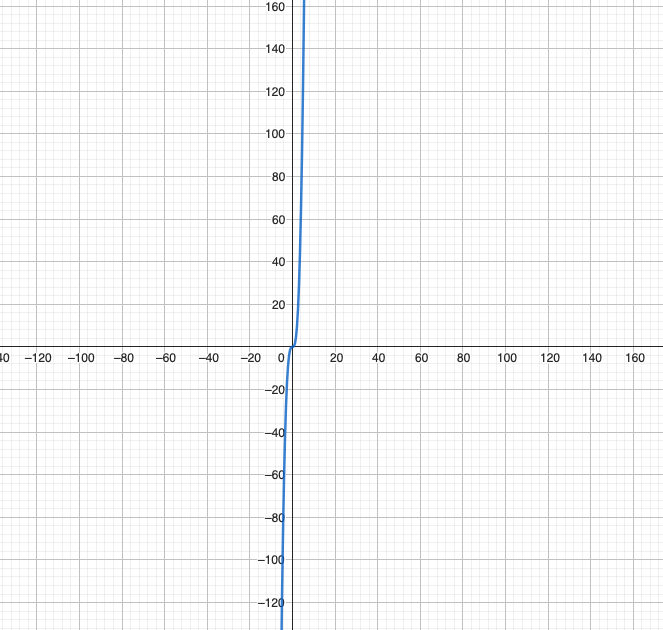
• p e p’ são equidistantes ao eixo da origem
  • a origem funciona como espelho
• a curva é oposta, mas simétrica
• o teste é ver se o f (x) = f (-x), por exemplo:
  • f (x ) = x³ → 2³ = 8
  • f (-x) = -x³ → 2³ = -8
    • os dois y (p e p’) deram -8 e 8

x	f(x)
0	0
1	+ e – 1
2	+ e – 8

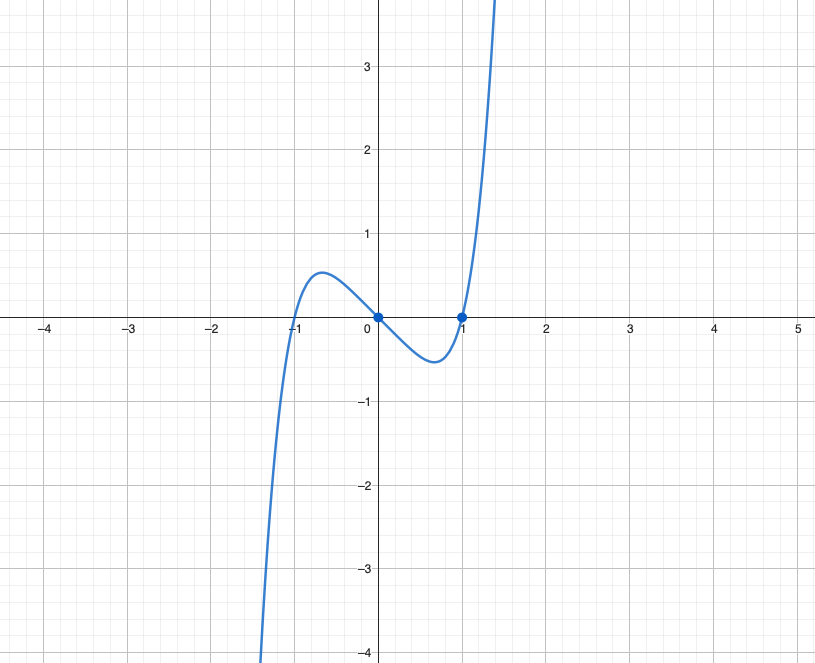
f (x) = x⁵ + x

• se fosse so o x⁵ saberiamos que é impar
• x → -x

f (x) = 2 – x⁴

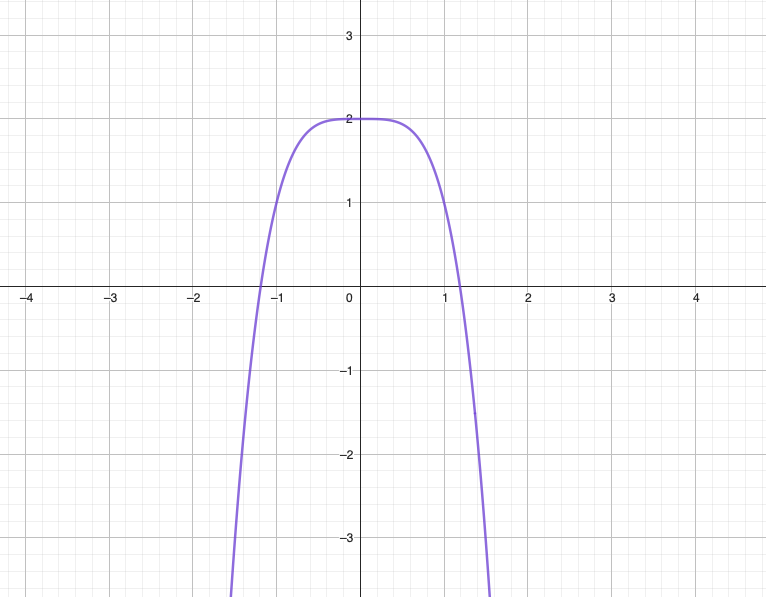
x	f(x)
0	2
1	1
2	-14

Funções crescentes e decrescentes

• como a função (o y) vai se comportar?
  • quando o f(x) aumenta, se acontecer para o f (x₂) ser maior, é crescente
    • x₂ > x₁
  • quando o f(x) diminui, se acontecer para o f (x₂) ser menor, é decrescente
    • x₂ < x₁

Aula-3-12Fev

Aula4-17Fev_4