Semana 3 – 23/08
ATENCAO
Questões de prova
– Vantagens/desvantagens do método de Bitterlich?
– 5 razoes para usar DAP?
– O que é mensuração?
Walter Bitterlich (Áustria, 1908-2008)
- método para obter estimativas da área basal por hectare em povoamentos florestais sem medir os diâmetros das árvores e nem lançar parcelas de área fixa.
- Vantagens:
- menor tempo gasto na amostragem;
- minimização de erros provenientes da demarcação incorreta da parcela;
- as estimativas podem ser obtidas através de aparelhos óticos de baixo custo.
- Desvantagens
- existência de sub-bosque abundante pode aumentar erros de inclusão visual
- não fornece variáveis importantes necessárias aos inventários (aspecto qualitativo do povoamento)
- fornece apenas a estimativa do número de árvores da área basal e do volume por ha.
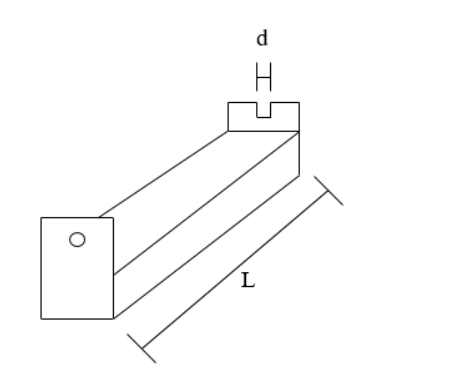
Barra de Bitterlich
- composta por uma haste de 1 m de comprimento, tendo um visor numa extremidade e na outra uma mira de 2 cm de largura
- “prova de numeração angular”
- postulado: “dando-se um giro de 360o, as árvores que apresentarem DAP superior ou igual a um ângulo conhecido e constante devem ser qualificadas. O número de árvores qualificadas (n) multiplicado por uma constante (K), denominada fator de área basal, fornecida por um instrumento apropriado, fornece diretamente a área basal por hectare (B/ha)”.
- relascópio de Bitterlich (espelho):
- Além da obtenção da área basal do povoamento em m2/ha, ele permite obtenção de alturas, diâmetros ao longo do fuste, distâncias horizontais e declividade do terreno. Além disso, possui vários fatores de área basal, que podem ser utilizados em função das características da floresta (declividade, densidade populacional, …).
Ilustrando:
Dando-se um giro de 360o, apenas três árvores foram qualificadas por apresentar DAP superior ou igual ao ângulo de visada (n=3)
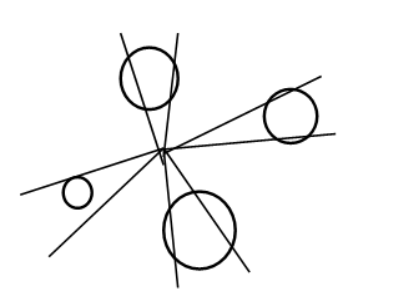
Supondo que o fator de área basal (K) utilizado foi igual a 1, a área basal por hectare naquele ponto de amostragem será:
B/ha = n . K
B/ha = 3 . 1 = 3 m2/ha
Agora para definir o K, precisamos usar outra fórmula.
Como descobrir o K?
K = 2500. (d/L)2
Exemplo:
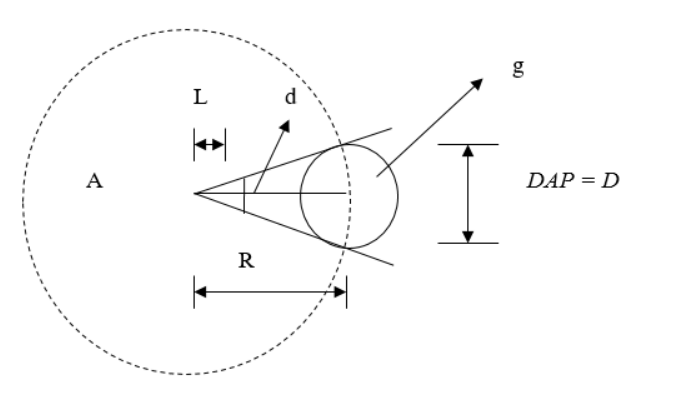
- R = distância máxima do observador até o centro da árvore para que esta seja qualificada (distância crítica), em m;
- d = abertura da mira, em cm;
- L = comprimento da barra de Bitterlich, em cm;
- g = área seccional, em m2; e
- A = área da parcela imaginária definida por R, em m2.
No exemplo, apenas uma árvore (n = 1) com DAP = D foi qualificada com uma barra de Bitterlich, em um giro de 360o.
De acordo com o postulado de Bitterlich, a área basal por hectare é dada por: B/ha = n . K
Como n = 1, conclui-se que o fator de área basal (K) pode ser obtido por 
.Dessa forma, para uma barra com d = 2 cm e L = 100 cm, o fator de área basal (K) deste instrumento será igual a 1, como mencionado anteriormente.
Definição do número de árvores e volume por hectare
De acordo com o princípio da “prova de numeração angular”, cada árvore contada representa uma quantidade em m2/ha, dependendo do fator de área basal (K) utilizado. Dessa forma, se for qualificada apenas uma árvore de área seccional (g) com fator K = 1 (d = 2 e L = 100 cm), a área basal será B = 1.1 = 1 m2/ha. No entanto, o número de árvores por hectare que cada árvore qualificada representa (N/ha) será:
O volume por hectare que cada árvore qualificada representa é dado, por sua vez, através da seguinte expressão:
.png)
em que 
é o volume estimado da árvore qualificada.
Exercício em aula:
Dados referentes a um ponto de amostragem obtidos com um fator de área basal (K) igual a 1:
Vai precisar utilizar a fórmula
V/ha = Vest.N/ha
N/ha = K/ As ou g
g = DAP2.π/40000
AB = K.n
Resposta:
- AB = K.n
AB = 1.10 (que é o número de árvores q aparecem na tabela acima)
AB = 10m2.ha-1 - Na tabela, agora vamos ter que descobrir o g (m2) e o N/ha
Ver no caderno (usar calculadora)
| Ponto (No) | Árvore (n) | DAP (cm) | Altura (m) | g (m2) g = DAP2.π/40000 | N/ha |
|---|---|---|---|---|---|
| 1 | 10,5 | g = (10,5)2.π/40000 g = 0,0087 m2 | N/ha = K/ As ou g N/ha = 1/0,0087 N/ha = 114,94m2.ha-1 | ||
| 2 | 12 | g = (12)2.π/40000 g = 0,0113 m2 | N/ha = K/ As ou g N/ha = 1/0,0113 N/ha = 88,50m2.ha-1 | ||
| 3 | 20,5 | g = (20,5)2.π/40000 g = 0,03306 m2 | N/ha = K/ As ou g N/ha = 1/0,03306 N/ha = 30,30m2.ha-1 | ||
| 4 | 22 | g = (22)2.π/40000 g = 0,0380 m2 | N/ha = K/ As ou g N/ha = 1/0,0380 N/ha = 26,32m2.ha-1 | ||
| 5 | 10,5 | g = (10,5)2.π/40000 g = 0,0087 m2 | N/ha = K/ As ou g N/ha = 1/0,0087 N/ha = 114,94m2.ha-1 | ||
| 6 | 12 | g = (12)2.π/40000 g = 0,0113 m2 | N/ha = K/ As ou g N/ha = 1/0,0113 N/ha = 88,50m2.ha-1 | ||
| 7 | 10 | g = (10)2.π/40000 g = 0,0079 m2 | N/ha = K/ As ou g N/ha = 1/0,0079 N/ha = 126,58m2.ha-1 | ||
| 8 | 20 | g = (20)2.π/40000 g = 0,0314 m2 | N/ha = K/ As ou g N/ha = 1/0,0314 N/ha = 31,85m2.ha-1 | ||
| 9 | 13 | g = (13)2.π/40000 g = 0,0133 m2 | N/ha = K/ As ou g N/ha = 1/0,0133 N/ha = 75,19m2.ha-1 | ||
| 10 | 11 | g = (11)2.π/40000 g = 0,0095 m2 | N/ha = K/ As ou g N/ha = 1/0,0095 N/ha = 105,26m2.ha-1 | ||
Saiba mais:
http://www.mensuracaoflorestal.com.br/capitulo-7-principio-de-bitterlich
ppt usado em aula