Empilhada
- é o volume de madeira roliça, em que, além do volume sólido de madeira, estão incluídos os espaços vazios, normais entre as toras e toretes. Este volume é medido por uma unidade chamada estéreo ou estére (st).
- 1 st = 0,7 m3 de madeira empihada
- um estéreo consiste na quantidade de madeira contida em uma pilha de 1 x 1 x 1, cujas toras variam em área seccional, curvatura e forma
- V = x.y.z
- média do comprimento das toras X comprimento da pilha X média da altura da pilha
Fator para expressar a conversão
- fator de cubicação: obtido pelo volume sólido em métro cúbico dividido pelo volume empilhado < 1,0
- Fc = Volume Sólido (m3) / Volume Empilhado (st) < 1,0
- o
Questão de prova
Fatores que afetam o empilhamento de madeira
- diâmetro e comprimento da tora
- espessura da casca
- a forma de empilhamento (manual ou mecanizado)
- tempo de permanência no campo na forma de tora
Exemplo 1
Em uma pilha de toras cujo Vsmalian foi de 0,68m3 e a pilha é 1,40m x 1,10m x 0,80m. Quais os fatores de cubicação e empilhamento?
Vempilhadost = x.y.z m3
Vempilhadost = 1,40 x 1,10 x 0,80
Vempilhadost =1,2320m3
Fator de cubicação = Vsmalian / Vempilhadost
Fator de cubicação = 0,68 / 1,2320
Fator de cubicação = 0,55
Fator de empilhado = Vempilhadost / Vsmalian
Fator de cubicação = 1,2320 / 0,68
Fator de cubicação = 1,81
Exemplo 2
A pilha é 2,00m x 3,00m x 1,50m, utilizou-se um fator de cubicação igual Fc = 0,60 para obter o volume sólido de madeira (m3).
a) Qual o volume sólido de madeira da pilha?
Vempilhadost = x.y.z m3
Vempilhadost = 2,00 x 3,00 x 1,50 m3
Vempilhadost = 9 m3
Fator de cubicação = Vsmalian ou solido / Vempilhadost /
0,60 = Vsólido / 9
Vsólido = 9 x 0,6
Vsólido = 5,4 m3
b) Considerando que a pilha de madeira continha 1/4 de espaços vazios, qual seria o volume sólido de madeira?
Vsólido = 9 x 0,75 m3
Vsólido = 6,75 m3
Volume de madeira laminada
É importante para poder saber quantos compensados podem ser construídos a partir de uma árvore ou de um grupo de árvores. A tora é laminada até que se torne um cilindro perfeito.
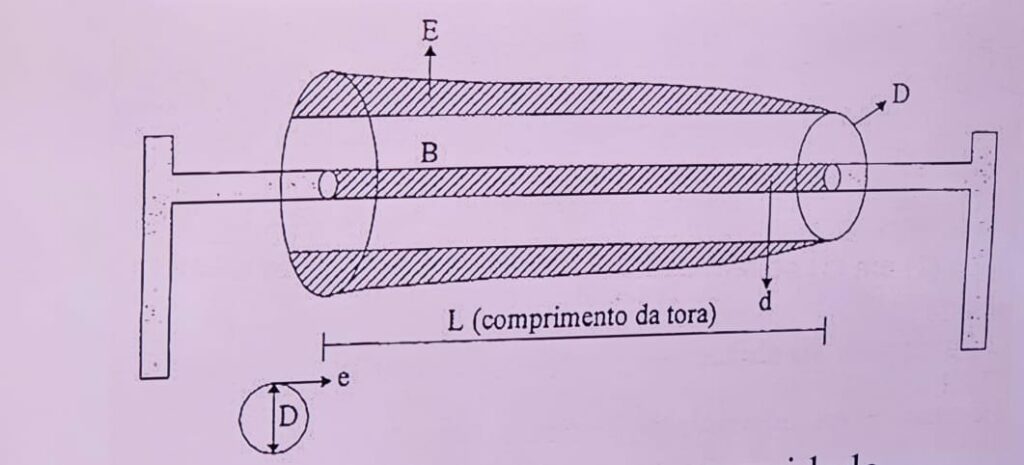
- D diâmetro do menor lado
- d miolo nao aproveitável (nao excede 5cm)
- E = parte da árvore não aproveitável para laminação
- B = parte a ser laminada
- e = espessura do laminado
Desejando-se o volume de madeira a ser desenrolada (VL) basta subtrair o volume do cilindro definido por (D), daquele definido por (d).
VL = (D2.π / 4 ou 40000) – (d2.π / 4 ou 40000) x L
Quantidade de madeira laminada
Q = (D2.π / 4 ou 40000) – (d2.π / 4 ou 40000) / e
Superfície de madeira laminada
S = Q. L
Exemplo 3
Deseja-se saber, de um tronco com 2m de comprimento, diâmetro sem casca na menor extremidade de 40cm, quantos compensados de 2m por 2m podem ser obtidos, se cada lâmina tem 2mm de espessura, e cada compensado é formado pela colagem de 4 destas lâminas. O miolo não laminado será de 4cm.
D = 40cm
d = 4cm
L = 200cm
e = 2mm -> 0,002
a) Volume de madeira laminada (VL)?
VL = (D2.π / 4 ou 40000) – (d2.π / 4 ou 40000) x L
VL = (402.π / 40000) – (42.π / 40000) x 200
VL = (0,1257 – 0,0013) x 2
VL = 0,1244 x 2
VL = 0,2488
b) Quantidade de madeira laminada (Q)?
Q = (D2.π / 4 ou 40000) – (d2.π / 4 ou 40000) / e
Q = 0,1244 / 0,002
Q = 62,2 laminados
c) Superfície de madeira laminada (S)?
S = Q. L
S = 62,2 x 2
S = 124,4 m2
*tem-se que os compensados serão de 2m por 2m, ou seja 4m2
c) Número de compensados?
*tem-se que os compensados serão de 2m por 2m, ou seja 4m2
*descobrimos que a área da superfície laminada é de 124,4 m2, o que dividido por 4m2, dá 31,1 lâminas
*tem-se que para cada compensado são necessárias 4 lâminas
31 laminas / 4 = 7,8 compensados
Volume da madeira serrada
É contabilizada de duas maneiras: por agrupamentos de peças individuais de tamanhos iguais, que podem ou não estar agrupados em fardos ou pacotes.
Madeira de tamanho uniforme
Para a determinação do volume de fardos, é necessário conhecer o volume e o número de peças
VP = E x L x C
VF = VP x N
L = largura (m); E = espessura (m); C = comprimento (m); N = número de peças
Madeira de tamanhos variados
O cálculo do volume dos fardos (pacotes) de tamanho variado poderá ser feito das seguintes formas:
VP = E x L x C
VF = Σ VP
L = largura (m); E = espessura (m); C = comprimento (m); N = número de peças
VF = L x lgx x (h -Σ e)
Exemplo:
Considerando uma tábula de madeira com dimensões de 2cm de espessura, 30cm de largura e 4m de comprimento, calcule:
a) Volume em m3 de duas dúzias e meia de tábuas (4 casas decimais)
e = 2cm
L = 30cm
C = 4m
Pacote: 30 peças
VP = E x L x C
VP = 0,02m x 0,3m x 4m = 0,0240m3
VF = 0,0240 x 30 = 0,7200m3
b) Número de tábuas necessárias para fazer um piso de madeira de 6m x 8m (1 casa decimal)
Área a ser coberta: 6×8 = 48m2
1 peça = 0,3 x 4 = 1,2m2
Peças necessárias = 48 / 1,2 = 40 tábuas
Saiba mais: