Relação hipsométrica – altura versus diâmetro

• estimativa para florestas plantadas: com plantas da mesma idade
  • medições frequentes em povoamentos jovens
• é definida como a relação existente entre a altura e o diâmetro da árvore. Tem grande significado prático no sistema de coleta de informações
  
• tendo uma amostra de dados de diâmetros e alturas, é possível obter uma relação matemática que permite estimar as alturas de toda a população ou parte dela
  
• é de fundamental importância nos procedimentos de inventário florestal
  
• economia de recursos, sem que haja perda de precisão

Fatores que influenciam a relação hipsométrica

• densidade: depende do estrato em que pertence a árvore. nas árvores dominantes a altura é pouco afetada, diferente em árvores dominadas
  
• tamanho da copa: quanto maior a copa, menor a razão altura-diâmetro
  
• espécie

Alguns modelos matemáticos

H = β₀ + β₁ x DAP + ε
ou
lnH = β₀ + β₁ x lnDAP + ε

• H ou lnH= variável dependente ( y = a + bx, equivalente ao y)
• DAP ou lnDAP = variável independente ( y = a + bx, equivalente ao x)
• β = coeficientes de regressão
• ε = erro aleatório

Método dos Mínimos Quadrados Ordinários (MMQO) para chegar aos valores de β₀ e β₁

β₁ = Σxy – Σx. Σy / n  ÷ Σx² – (Σx₁)²/n
β₀ = ~y – β₁.x̅

Exemplo:

Tabela dada em aula. Números em verde e azul foram calculados, por alunos, por calculadora científica no SD mode (fiz no Excel, preciso refazer na calculadora para treinar para a prova)

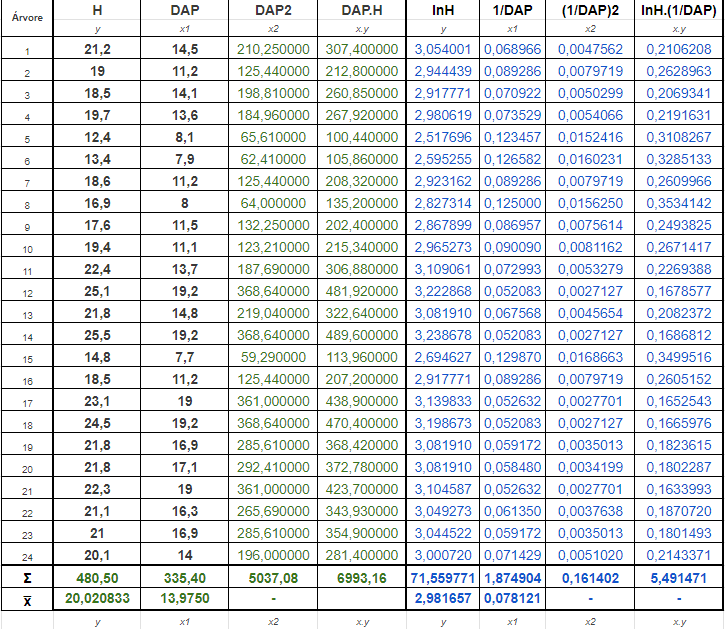
Usando a primeira fórmula H = β₀ + β₁ x DAP + ε, vamos calcular o β₀ e β₁ a partir do H (como y) e do DAP (como x), usando os números, somatórias e médias em verde calculados na tabela acima

β₁ = Σxy – Σx. Σy / n  ÷ Σx² – (Σx)²/n
β₁ = 6993,16 – 335,40 x 480,50 / 24  ÷ 5037,08 – (335,40)²/24
β₁ = 6993,16 – 161159,70/ 24  ÷ 5037,08 – 112493,16/24
β₁ = 6993,16 – 6714,9875  ÷ 5037,08 – 4687,215
β₁ = 278,172500  ÷ 349,865
β₁ = 0,795085

—–
β₀ = ~y – β₁.x̅
β₀ = 20,020833 – 0,795085.(13,975)
β₀ = 20,020833 – 11,111313
β₀ = 8,909520

AGORA VAMOS VOLTAR A FÓRMULA DA RELAÇÃO H em função do DAP.

H = β₀ + β₁ x DAP + ε
H = 8,909520 + 0,795085 x DAP

— sendo DAP de 10cm
H = 8,909520 + 0,795085 x 10
H = 8,909520 + 7,95085
H = 16,86m

— sendo DAP de 15cm
H = 8,909520 + 0,795085 x 15
H = 8,909520 + 11,926275
H = 20,84m

— sendo DAP de 18cm
H = 8,909520 + 0,795085 x 18
H = 8,909520 + 14,311530
H = 23,22m

Usando a primeira fórmula lnH = β₀ + β₁ x lnDAP + ε, vamos calcular o β₀ e β₁ a partir do lnH (como y) e do lnDAP (como x), usando os números, somatórias e médias em azul calculados na tabela acima.

β₁ = Σxy – Σx. Σy / n  ÷ Σx² – (Σx)²/n
β₁ = 5,491471 – 1,874904 x 71,559771 / 24  ÷ 0,1614019 – (1,874904)²/24
β₁ = 5,491471 – 134,167721 / 24  ÷ 0,1614019 – 3,515266/24
β₁ = 5,491471 – 5,590322  ÷ 0,1614019 – 0,146469
β₁ = -0,098851 ÷ 0,0149324
β₁ = -6,619883

—–
β₀ = ~y – β₁.x̅
β₀ = 2,981657 – (-6,619883) .(0,078121)
β₀ = 2,981657 – (-0,517520)
β₀ = 3,498809