- Os blocos ao acaso constituem o tipo de delineamento mais utilizado em experimentos no campo;
- Princípios:
- repetição
- casualização
- controle local
- Quando se desconfia de qualquer heterogeidade ambiental, por medida de segurança, é preferível a utilização de blocos.
- É utilizado quando as unidades experimentais são agrupadas (blocos)
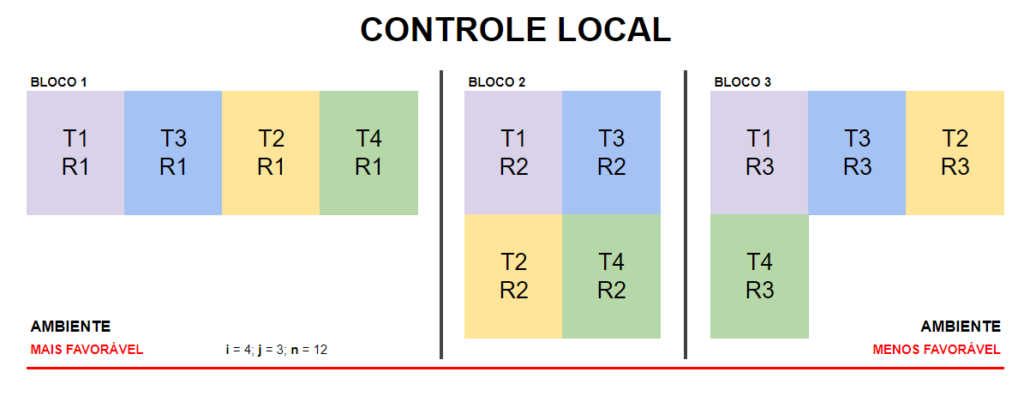
- Por exemplo, eu sei que em uma área o ambiente não é bom (característica do solo, da luz, da umidade); então se eu de repente só tiver 2 tratamentos/culturas de 4 naquela área, posso concluir que aqueles 2 tratamentos/culturas não são bons, mas de fato era ambiente que não era bom.
- para ter certeza no experimento, criamos blocos experimentais que são instalados em diferentes ambientes homogêneos mais ou menos do mesmo tamanho, colocando em cada um desses blocos todos os 4 tratamentos/culturas de forma casualizada;
- assim é possível controlar e reduzir o erro de que algum tratamento/cultura seja favorecido.
- Algumas vezes não é possível sortear todos os tratamentos dentro de cada bloco por motivos como:
- tamanho da parcela, tamanho dos blocos, número elevado de tratamentos etc
- nestes casos, tem-se delineamentos com blocos incompletos
Vantagens:
- Adapta-se a muitas situações de campo;
- Controla as diferenças que ocorrem nas condições ambientais;
- A estimativa da variância residual ou erro experimental é mais exata, uma vez que a variação ambiental é controlada.
Desvantagens:
- Diminui o número de graus de liberdade do resíduo;
- Necessidade de formar blocos homogêneos;
- Pode limitar o número de tratamento a serem utilizados, devido à exigência de homogeneidade dentro dos blocos
Uso:
- Em áreas heterogêneas capazes de serem estratificadas em áreas menores e homogêneas;
- Os critérios para o agrupamento podem ser características ambientais: faixa de terra, localização geográfica, intensidade de luz, tipologia florestal, declividade, ala da estufa ou do viveiro, um período de tempo, faixa de idade, tipo de floresta, faixa de peso etc.
Arranjo de campo e sorteio:
- Distribuição aleatória dos tratamentos;
- Cada bloco deve ser tratado independente dos demais;
- Os blocos devem ser alocados de forma aleatória também no campo.
yij = m + ti + bj + eij
- yij = valor observado no tratamento i (i = 1, 2, … , i) e no bloco j (j = 1, 2, … j)
- m = média geral de todas as observações do experimento
- ti = efeito do tratamento i.
- bj = efeito do bloco j
- eij = erro associado à observação yij, ou efeito dos fatores não-controlados sobre a observação yij.
Fontes de variação:
- Tratamentos (causa conhecida)
- Blocos
- Resíduos/ Erro experimental (causa não desconhecida)
As fontes de variação em um experimento em blocos casualizados são:
- a variação intencional constituída pelos tratamentos e introduzida pelo pesquisador;
- o controle local constituído pelos blocos;
- a variação aleatória ou devida a fatores não controlados, denominada resíduo.
Exemplo prático
- Uma área heterogênea foi dividida em quatro áreas homogêneas menores nas quais foram testados o plantio de 4 variedades de Cupuaçu.
- Cada parcela era composta de 5 plantas (parcela composta) e a variável resposta foi o peso médio dos frutos, obtidos 6 anos após o plantio.
Croqui do campo:
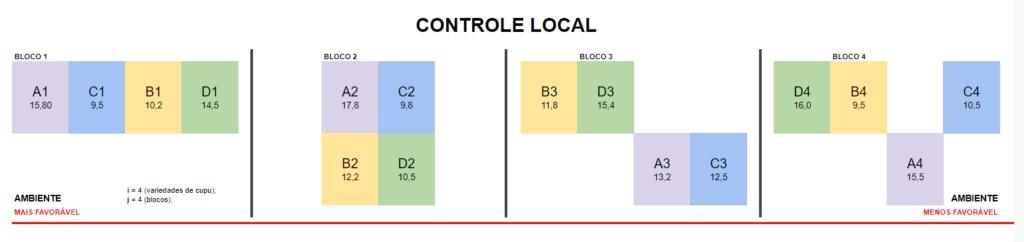
Dados tabulados:
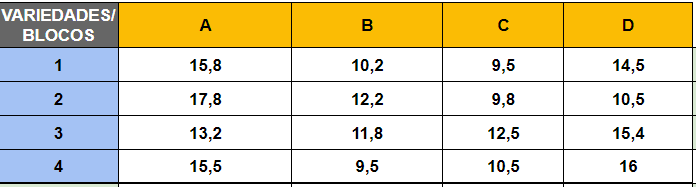
Cálculos detalhados:
PASSO 1 – Calcular o valor da correção
- Limpar memória da calculadora
- Entrar todos os valores individuais
15,817,8
13,2
… 16
- No final desse passo aparecerá na calculadora N = 16
- Calcular o total y•• (Σx) em
204,7 - Elevar o resultado ao quadrado
41902,09 - Dividir por n (16)
2.618,88 → valor da correção
PASSO 2 – Calcular o SQT Total
- Calcular Σx2
2.729,79 - Subtrair o valor da correção -(4.268,44)
110,91
PASSO 3- Calcular o SQT Tratamento (coluna)
- Calcular a soma de cada tratamento (coluna por coluna)
15,817,8
13,2
15,5
= n4
- y•• (Σx) em
62,30 (coluna A); 43,70 (coluna B); 42,30 (coluna C); 56,40 (coluna D) - Elevar o resultado de cada coluna ao quadrado
3881,29 (coluna A); 1909,69 (coluna B); 1789,29 (coluna C); 3180,96 (coluna D) - Dividir o resultado de cada coluna por 4, que é j (blocos)
970,32 (coluna A); 477,42 (coluna B); 447,32 (coluna C); 795,24 (coluna D) - Somar os resultados das somas de quadrados dividido por j
2690,31 - Subtrair o valor da correção -(2618,88)
71,43
PASSO 4 – Calcular o SQBloco (linha)
- Calcular a soma de cada tratamento (coluna por coluna)
15,810,2
9,5
14,5
= n4
- y•• (Σx) em
50 (linha 1); 50,3 (linha 2); 52,9 (linha 3); 51,50 (linha 4) - Elevar o resultado de cada coluna ao quadrado
2500 (linha 1); 2530,09 (linha 2); 2798,41 (linha 3); 2652,25 (linha 4)= - Dividir o resultado de cada coluna por 4, que é j (blocos)
970,32 (coluna A); 477,42 (coluna B); 447,32 (coluna C); 795,24 (coluna D) - Somar os resultados das somas de quadrados dividido por j
2620,19 - Subtrair o valor da correção -(2618,88)
71,43
PASSO 5 – Calcular o SQResíduo
- SQTotal (71,43) – [SQTrat (70,22) + SQBl (1,31)]
38,17
PASSO 6 – Calcular os Quadrados Médios
- Dividir as Somas dos Quadrados (SQ) do tratamento e do resíduo dividindo as
somas pelos respectivos Graus de Liberdade (GL)
SQTrat/ GLTrat → 71,4 / 3 = 23,81
SQBl / GLBl → 1,31 / 3 = 0,44
SQResíduo/ GLResíduo → 38,17 / 9 = 4,24
PASSO 7 – Calcular o valor de F
- Dividir o Quadrado Médio do Tratamento (QMTrat) pelo Quadrado Médio dos Resíduos (QMR)
QMTrat/ QMResíduos → 23,81/ 4,24 = 5,61
QMBloco/ QMResíduos → 0,44/ 4,24 = 0,10
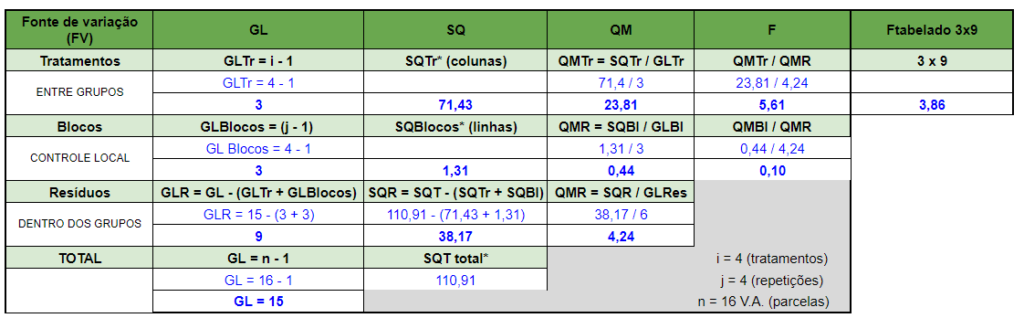
Ftratcalc > Ftabelado = rejeita H0
Fblococalc > Ftabelado = aceita H0
Saiba mais: