- não é um delineamento
- é uma forma de avaliar mais fatores em um experimento
Exemplo: 3 x 3 = 9 tratamentos
fator um: serão testados 3 tipos de mogno – brasileiro, senegalense, costa-do-marfim
fator dois: serão testados 3 tipos de adubação – com fósforo, com trichoderma, de controle
i = 9; com 4 repetições -> j = 4, logo n = 36 V.A.
Exemplo fitopatologia 2 x 2
- Fatorial 1: substrato com tratamento de trichoderma ou sem tratatamento
- Fatorial 2: semente com tratamento de trichoderma ou sem tratamento
i = 2 x 2 = 4;
j = 15;
n = 60.
Na tabela de ANOVA, o FV seria
- Fator 1 (substrato com/sem tratamento)
- Fator 2 (semente com/sem tratamento)
- F1 x F2
- Resíduo
- Total
Hipóteses da análise de variância
Fator 1
- H0 os níveis tem o mesmo efeito
- H1 tem efeitos diferentes
Fator B
- H0 os níveis tem o mesmo efeito
- H1 tem efeitos diferentes
Entre fatores A e B
- H0 as interações tem o mesmo efeito
- H1 pelo menos duas combinações tem efeito diferente
Modelo estatístico
Seja um experimento fictício em DIC com 3 repetições para analisar o efeito de calagem (Fator C) e da irrigação (Fator I) sobre o peso de plantas (kg/ planta/ parcela)
I = (2 x 2) = 4; j = 3; n = 12
| C0I0 | C1I0 | C0I1 | C1I1 | |
|---|---|---|---|---|
| Repetição 1 | 25 | 35 | 41 | 60 |
| Repetição 2 | 32 | 28 | 35 | 67 |
| Repetição 3 | 27 | 33 | 38 | 59 |
ANOVA = DIC
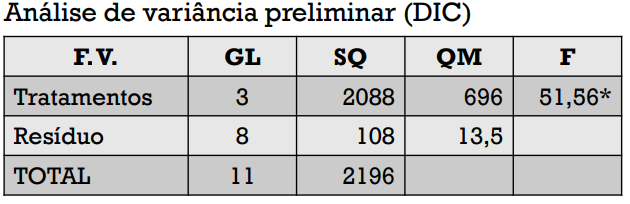
Conclusão: Os pesos das plantas cultivadas com os diferentes tratamentos não são iguais entre si.
Mas o experimento foi feito em esquema fatorial. Se o objetivo do trabalho é testar a interação C x I, a análise de variância deve ser desdobrada.
Contas
